Los números irracionales y la irracionalidad de la belleza

Quiero mostrar mi arrepentimiento y mi propósito de enmienda por todas las ocasiones en que ignoré a mi profe de matemáticas, todas las siestas culpables que me proporcionaron las clases en el sopor de mi estulticia, todas las ocasiones en las que me dije que esto era un entretenimiento de gente aburrida y rara, normalmente asocial y extravagante que no tenía amigos por ser insoportablemente tediosa. Quiero mostrar públicamente el error de juventud, entonar el mea culpa y que Pitágoras y sus seguidores en su magnanimidad sepan perdonarme. Ahora me embobo descubriendo la fascinante herramienta que inventaron nuestros ancestros para explicar el mundo y que hoy usamos con alegría por todas partes sin percatarnos de ello. Con esa precisión milimétrica que ordena todo y nos hace estar un poco menos cerca del caos.

Las mates y la ciencia son modos de aproximarnos al mundo que algunos tratamos de utilizar siempre que nos es posible. Existen otros modos pero no son tan fiables. Hay un anhelo de belleza en nosotros que se expresa en la admiración por ella y por disfrutarla. Muchas veces nos conformamos con admirarla, otras tratamos de crearla y a los amantes de las matemáticas les gusta explicarla.

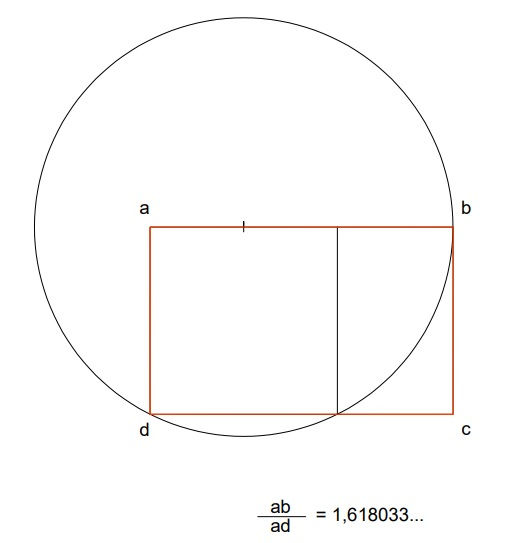
Dicen los matemáticos que los números irracionales son aquellos que no pueden representarse como “razón” de dos números, esto es, que no podemos encontrar ningún par de números que dividiéndoles den como resultado estos números tan curiosos. Por ejemplo √2 (1,4142…) es un número que tiene infinitos decimales que no se repiten, por lo que no puede representar como razón de dos números. Lo mismo ocurre con √3 (1,7320…), con el número “pi” (3,1415…), el número “e” (2,7182…) o el llamado número áureo ɸ (1,6180…)

Los constructores de catedrales, además de buenos arquitectos y artesanos, cabales ingenieros y artistas, eran conocedores de la geometría (medida de la tierra) y de las matemáticas. Estaban convencidos de que para crear algo útil y bello tenían que usar la geometría y las matemáticas porque la naturaleza, en sus formas más bellas, lo hacía. En realidad era la voluntad de Dios expresada en las maravillas de la naturaleza. Conocían los números irracionales y los usaban con destreza para asombrarnos.

Si dibujamos dos círculos de cualquier radio juntos de tal manera que cada uno pase por el centro del otro, tenemos la vesica piscis o mandorla. Esta figura aparece en el arte y arquitectura de mil maneras diferentes:

Curiosamente, seguimos usando los números irracionales para muchos objetos cotidianos que también siguen proporciones basadas en números irracionales. Las tarjetas de crédito tienen unas dimensiones normalizadas (ISO 7810) que cuando divides el lado mayor entre el menor nos da 1,6: el número áureo. Cajetillas de tabaco, teléfonos móviles, cajas de embalaje, tarjetas de visita comerciales. Por mi parte ando midiendo como loco cualquier rectángulo que me encuentro por ahí para verificar esta tendencia oculta.

La Escalera Dorada de la Catedral de Burgos proyectada por Diego de Siloé tiene oculto también el número áureo. Los artistas y arquitectos del pasado no dejaban al azar las decisiones que hacían bello su trabajo.

Se dice que, en realidad no hacemos otra cosa que copiar a la naturaleza, cuando pretendemos crear nuestros ingenios. Las flores de los castaños nos dan pistas.

El triángulo dorado o triángulo áureo es un triángulo isósceles (dos lados iguales) tal que la longitud de los lados iguales dividida por la longitud del otro lado da 1,6180, es decir el número áureo.

No sabemos si los veranos en los paseos arbolados burgaleses fueron la inspiración para dar forma a la fachada occidental de la Catedral a Hans von Köln, o Juan de Colonia para los amigos, que convivieron con él sobre el 1448 y se daba paseos con ellos buscando la sombra para hacer más llevaderos los veranos en unas tierras mucho más soleadas que las que le vieron nacer.

Al genial Gaudí le llaman el arquitecto de la naturaleza porque era su fuente de inspiración. Muy pronto aplicó su genio a su obra cuya síntesis podría resumirse en tres elementos presentes en casi todas sus creaciones: la columna extraplomada (como los árboles en los bosques, que muchas veces no crecen perfectamente verticales), el trencadís (los mosaicos troceados) y el arco formado por un polígono funicular invertido, que sería la figura que obtenemos cuando sujetamos una cuerda con las dos manos y dejamos que su peso forme esta curiosa curva (catenaria). Ilustrar la obra de Gaudí requiere mucho afán por lo extensa. Entrar en su universo es todo un reto que el común de los turistas, cuando visita sus obras emblemáticas, aprecia superficialmente quedándose en ese poso bello que emociona. Cuando se mira su obra con ojos de científico, esa emoción torna en admiración y en pasión por descubrir más.

Chiti del Amo en su blog, que aquí Chiti del Amo enlazo, hace un resumen ilustrado muy recomendable que puede ser el principio de un fantástico viaje. Suerte y buen camino.

Y como buen descendiente de alarife no puedo dejar de citar la profunda impresión que me produjo ver por primera vez la mezquita de Córdoba cuando ya venía de casa un poco admirado por las yeserías mudéjares, grecas árabes y las finas huellas que dejaron en este carácter austero castellano las finuras ornamentales de nuestros antepasados moros.

Resulta que encima de la tumba del baqueteado Cid se encuentra la torre más admirable de la Catedral de Burgos: el cimborrio. Una de las más bellas linternas construidas para un edificio «que más parece obra de ángeles que de hombres».

Pues resulta que nuestros astutos canteros y escultores dirigidos por Juan de Vallejo y Francisco de Colonia no se la jugaron y usaron la misma idea que sus antepasados arquitectos musulmanes: la proporción cordobesa, o el rectángulo cordobés.

Rectángulo cordobés

Todas estas maravillas ocultas las descubrí bastante tarde. Pese a todo, sigo contando con los dedos para saber los días que faltan para el próximo viernes. Me lío con las vueltas que me da mi frutera en el mercado cuando pago la compra y no me acuerdo de las operaciones que resuelven una raíz cuadrada. Si te doy la fecha de mi nacimiento cuando me preguntan es porque me cuesta hacer la cuenta de los años que tengo: Te dejo a ti el trabajo.

Admiraba a mi joven padre cuando le acompañaba a una de sus obras como ayudante y calculaba, en cuestión de segundos, la cantidad de ladrillos que llevaría un paño sabiendo las medidas de largo y alto. Cuando me pedía atar los extremos de una cuerda en una parcela y con tres estacas clavadas medir 3, 4 y 5 para sacar el ángulo recto que formarían las futuras paredes. Creo que me costó mucho tiempo deducir que estaba usando un triángulo rectángulo y uno de los teoremas más conocidos de la historia de la humanidad. Y sobre todo, aún me sigue admirando esa capacidad que tenía para decidir la huella y contrahuella que ha de tener una escalera para subir de un piso a otro sin que cada escalón sea un tropezón o una cuesta imposible. Las escaleras que hacía mi padre eran muy cómodas. Las calculaba en cuestión de minutos.

Hoy siento esa irracional atracción por la belleza y por las matemáticas. Ahora no protesto cuando me quieren llevar a ver una exposición de arte abstracto o “performances artísticas” de oscuros significados. Soy capaz de escuchar con la misma cara que tienen las vacas al mirar el tren que pasa, una conferencia de arte impresionista búlgaro, y parecer que estoy profundamente “impresionado”. Y sobre todo soy capaz de no juzgar bajo mi visión aldeana del mundo cualquier manifestación artística que veo por ahí. El precario somier oxidado que ató con alambres al poste, el paisano, para cerrar la huerta en el pueblo, al tío le pareció bonito. ¡Joé! ¡Quién soy yo para juzgarlo!

INOS

(Todas las imágenes son del autor)